Atom orbitali

Birinchi beshta atom orbitallarining shakllari: 1s, 2s, 2p _x, 2p _y va 2p _z . Ikki rang har bir mintaqadagi to'lqin funksiyasining fazasini yoki belgisini ko'rsatadi. Har bir rasm bitta elektronning koordinatalariga bog'liq boʻlgan

ψ(x, y, z)

funksiyasining domen rangidir. Ehtimollik zichligini to'g'ridan-to'g'ri ko'rsatadigan

ψ(x, y, z) 2

funksiyaning cho'zilgan shaklini ko'rish uchun quyidagi d-orbitallarning rasmlariga qarang.

Atom nazariyasi va kvant mexanikasida atom orbitali atomdagi elektronning joylashuvi va to'lqinsimon harakatini tavsiflovchi funksiyadir.^[1] Bu funksiya atom yadrosi atrofidagi har qanday aniq mintaqada atomning istalgan elektronini topish ehtimolini hisoblash uchun ishlatilishi mumkin. Atom orbital atamasi, shuningdek, orbitalning o'ziga xos matematik shakli bilan bashorat qilinganidek, elektron mavjudligini hisoblash mumkin boʻlgan jismoniy mintaqa yoki bo'shliqqa ham tegishli bo'lishi mumkin.^[2]

Atomdagi har bir orbital n, ℓ va ml uchta kvant sonlarining qiymatlari to'plami bilan tavsiflanadi, ular mos ravishda elektronning energiyasiga, burchak momentumiga va burchak momentum vektor komponentiga (magnit kvant soni) mos keladi. Magnit kvant soniga muqobil ravishda orbitallar ko'pincha bog'langan garmonik polinomlar bilan belgilanadi (masalan, xy, x² − y²). Har bir bunday orbital maksimal ikkita elektron bilan band bo'lishi mumkin, ularning har biri o'ziga xos spin proyeksiyasiga ega. $m_{s}$ . Oddiy s orbital, p orbital, d orbital va f orbital nomlari mos ravishda burchak momentum kvant soni $ℓ = 0, 1, 2,$ va $3$ boʻlgan orbitallarga tegishli. Bu nomlar qiymati bilan birga n, atomlarning elektron konfiguratsiyasini tavsiflash uchun ishlatiladi. Ular dastlabki spektroskopistlar tomonidan ishqoriy metall spektroskopik chiziqlarning ma'lum seriyalarini s arfa, p rinsipal, d iffuse va f undamental sifatida tavsiflashdan olingan. ℓ > 3 uchun orbitallar alifbo tartibida davom etadi (g, h, i, k, ...),^[3] qoldirmasdan j^[4]^[5] chunki baʼzi tillarda “i” va “j” harflari farqlanmaydi.^[6]

Atom orbitallari atom orbital modelining (yoki elektron buluti yoki to'lqin mexanikasi modeli) asosiy qurilish bloklari bo'lib, materiyadagi elektronlarning submikroskopik harakatlarini vizualizatsiya qilish uchun zamonaviy asosdir. Ushbu modelda atomning elektron buluti oddiyroq vodorodga o'xshash atom orbitallarining hosilasi boʻlgan elektron konfiguratsiyada (taxminan) tuzilgan deb qaralishi mumkin. Davriy jadvalning bo'limlaridagi 2, 6, 10 va 14 elementli bloklarning takroriy davriyligi tabiiy ravishda s, p, d va f orbitallarning to'liq to'plamini egallagan elektronlarning umumiy sonidan kelib chiqadi, lekin undan yuqori bo'lsa ham. n kvant sonining qiymatlari, ayniqsa atom musbat zaryadga ega bo'lsa, ba'zi kichik qobiqlarning energiyalari juda o'xshash bo'ladi va shuning uchun ularni elektronlar bilan to'ldirish tartibi (masalan, Cr = [Ar] 4s ¹ 3d ⁵ va Cr ²⁺ = [Ar]3d ⁴) faqat bir oz ixtiyoriy ravishda ratsionalizatsiya qilinishi mumkin.

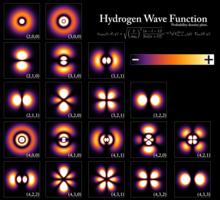
Elektron xossalari

Kvant mexanikasi va eksperimental topilmalar rivojlanishi bilan (masalan, elektronlarning ikki yoriqli difraksiyasi) yadro atrofida aylanayotgan elektronlarni zarrachalar sifatida toʻliq tasvirlab boʻlmasligi, balki ularni toʻlqin-zarracha ikkilikligi bilan izohlash zarurligi aniqlandi. Shu ma'noda elektronlar quyidagi xususiyatlarga ega:

Zarrachaga o'xshash xususiyatlar:

Yadro atrofida aylanadigan elektronlar soni faqat butun son bo'lishi mumkin.
Elektronlar zarralar kabi orbitallar orasidan sakrab o'tadi. Misol uchun, agar bitta foton elektronlarga urilsa, natijada faqat bitta elektron holatni o'zgartiradi.
Elektronlar zarrachaga o'xshash xususiyatlarni saqlab qoladi, masalan: har bir to'lqin holati uning elektron zarrasi bilan bir xil elektr zaryadiga ega. Har bir to'lqin holati superpozitsiyasiga qarab bitta diskret spinga ega (yuqoriga yoki pastga aylanish).

Orbital turlari

Atom orbitallari vodorodga o'xshash "orbitallar" bo'lishi mumkin, ular vodorodga o'xshash "atom" (ya'ni, bitta elektronli atom) uchun Shredinger tenglamasining aniq echimi hisoblanadi. Shu bilan bir qatorda, atom orbitallari bir elektronning (ya'ni, orbitallarning) koordinatalariga bog'liq boʻlgan, ammo atom yoki molekuladagi barcha elektronlarning bir vaqtning o'zida koordinatalariga bog'liq boʻlgan to'lqin funksiyalarini yaqinlashish uchun boshlang'ich nuqta sifatida ishlatiladigan funksiyalarni anglatadi. Orbitallar uchun tanlangan koordinatalar tizimi odatda atomlarda sferik koordinatalar $(r, θ, φ)$ va koʻp atomli molekulalarda dekart $(x, y, z)$ hisoblanadi. Bu yerda sferik koordinatalarning afzalligi shundaki, orbital to'lqin funksiyasi uchta omilning har biri bitta koordinataga bog'liq boʻlgan ko'paytmasidir: $ψ (r, θ, φ) = R (r) Θ(θ) Φ(φ)$ . Atom orbitallarining burchak omillari D $Θ(θ) Φ(φ)$ s, p, d va boshqalarni hosil qiladi. $Y ℓm (θ, φ)$ sferik harmonikalarning haqiqiy birikmalari vazifasini bajaradi (bu yerda ℓ va m kvant sonlari). Radial funksiyalar uchun odatda uchta matematik shakl mavjud Ko'p elektronli atomlar va molekulalarning xususiyatlarini hisoblash uchun boshlang'ich nuqta sifatida tanlanishi mumkin boʻlgan $R (r)$ :

Murakkab orbitallar

Fizikada eng keng tarqalgan orbital tavsiflar vodorod atomining eritmalariga asoslanadi, bu yerda orbitallar radial funksiya va sof sferik harmonik o'rtasidagi mahsulot bilan beriladi. Kvant raqamlari va ularning mumkin boʻlgan qiymatlarini tartibga soluvchi qoidalar quyidagicha:

Asosiy kvant soni n elektronning energiyasini tavsiflaydi va har doim musbat butun sondir . Aslida, u har qanday musbat butun son bo'lishi mumkin, lekin quyida muhokama qilingan sabablarga ko'ra, katta raqamlar kamdan-kam uchraydi. Har bir atom, umuman olganda, n ning har bir qiymati bilan bog'liq boʻlgan ko'plab orbitallarga ega; bu orbitallar birgalikda ba'zan elektron qobiqlar deb ataladi.

Azimutal kvant soni ℓ har bir elektronning orbital burchak momentini tavsiflaydi va manfiy bo'lmagan butun sondir. n ba'zi bir butun son $n 0$ boʻlgan qobiq ichida ℓ munosabatni qanoatlantiradigan barcha (butun) qiymatlar bo'ylab diapazonda joylashgan. $0\leq \ell \leq n_{0}-1$ . Masalan, $n = 1$ qobiq faqat orbitallarga ega $\ell =0$ va $n = 2$ qobiq faqat orbitallarga ega $\ell =0$ va $\ell =1$ . ning ma'lum bir qiymati bilan bog'liq boʻlgan orbitallar to'plami ℓ ba'zan birgalikda subshell deb ataladi.

Magnit kvant soni, $m_{\ell }$ , elektronning ixtiyoriy yo'nalishdagi magnit momentini tavsiflaydi va har doim ham butun sondir. Subshell ichida qaerda $\ell$ ba'zi bir butun sondir $\ell _{0}$ , $m_{\ell }$ shunday diapazonda: $-\ell _{0}\leq m_{\ell }\leq \ell _{0}$ .

Yuqoridagi natijalarni quyidagi jadvalda umumlashtirish mumkin. Har bir katak pastki qavatni ifodalaydi va qiymatlarini sanab o'tadi $m_{\ell }$ ushbu pastki qavatda mavjud. Bo'sh hujayralar mavjud bo'lmagan pastki qavatlarni ifodalaydi.

	$ℓ = 0 (s)$	$ℓ = 1 (p)$	$ℓ = 2 (d)$	$ℓ = 3 (f)$	$ℓ = 4 (g)$	...
$n = 1$	$m_{\ell }=0$					...
$n = 2$	0	−1, 0, 1				...
$n = 3$	0	−1, 0, 1	−2, −1, 0, 1, 2			...
$n = 4$	0	−1, 0, 1	−2, −1, 0, 1, 2	−3, −2, −1, 0, 1, 2, 3		...
$n = 5$	0	−1, 0, 1	−2, −1, 0, 1, 2	−3, −2, −1, 0, 1, 2, 3	−4, −3, −2, −1, 0, 1, 2, 3, 4	...
...	...	...	...	...	...	...

Subshelllar odatda ular bilan aniqlanadi $n$ - va $\ell$ -qiymatlar. $n$ uning son qiymati bilan ifodalanadi, lekin $\ell$ harf bilan quyidagicha ifodalanadi: 0 's', 1 'p', 2 'd', 3 'f' va 4 'g' bilan ifodalanadi. Masalan, subshell haqida gapirish mumkin $n=2$ va $\ell =0$ "2s subshell" sifatida.

Har bir elektron, shuningdek, har bir elektronning spinini (yuqoriga yoki pastga aylantirish) tavsiflovchi spin kvant raqamiga ega s soni bo'lishi mumkin -1/2;+1/2

Pauli istisno printsipi shuni ko'rsatadiki, atomdagi ikkita elektron to'rtta kvant sonining bir xil qiymatlariga ega bo'lmaydi. Agar orbitalda uchta kvant soni (n, ℓ, m) uchun berilgan qiymatlarga ega ikkita elektron mavjud boʻlsa, bu ikki elektron spinida farq qilishi kerak.

Yuqoridagi konventsiyalar afzal qilingan o'qni nazarda tutadi (masalan, Dekart koordinatalaridagi z yo'nalishi) va ular ushbu afzal o'q bo'ylab afzal qilingan yo'nalishni ham nazarda tutadi. Aks holda $m = +1$ ni $m = -1$ dan ajratishning ma'nosi bo'lmaydi. Shunday qilib, model ushbu simmetriyalarga ega boʻlgan jismoniy tizimlarga qo'llanilganda eng foydali hisoblanadi. Stern-Gerlach tajribasi - atom magnit maydon ta'sirida - bunday misollardan birini beradi.^[7]

Haqiqiy orbitallar

orasidagi doimiy o'zgaruvchan superpozitsiyalarning animatsiyasi $p_{1}$ va $p_{x}$ orbitallar. Esda tutingki, bu animatsiya Kondon-Shortli faza konventsiyasidan foydalanmaydi.

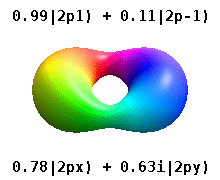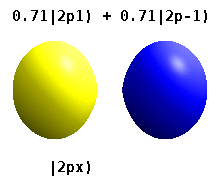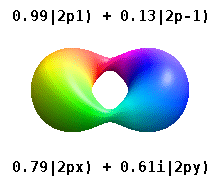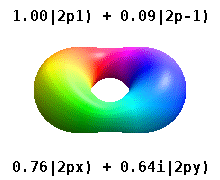
Orbitalar jadvali

Ushbu jadval 7s gacha boʻlgan barcha atom orbitallari uchun haqiqiy vodorodga o'xshash to'lqin funksiyalarini ko'rsatadi va shuning uchun davriy jadvaldagi barcha elementlarning asosiy holatidagi egallangan orbitallarni radiygacha va ba'zilari undan tashqarida qamrab oladi. "ps" grafiklari ikki xil rangda (o'zboshimchalik bilan qizil va ko'k) ko'rsatilgan - va + to'lqin funksiyasi fazalari bilan ko'rsatilgan. $p z$ orbitali $p 0$ orbitali bilan bir xil, ammo $p x$ va $p y$ $p +1$ va $p -1$ orbitallarining chiziqli birikmalarini olish natijasida hosil bo'ladi (shuning uchun ular $m = \pm1$ yorlig'i ostida keltirilgan).). Bundan tashqari, $p +1$ va $p -1$ $p 0$ bilan bir xil shaklga ega emas, chunki ular sof sferik harmonikalardir .

	s ( $ℓ = 0$ )	p ( $ℓ = 1$ )			d ( $ℓ = 2$ )					f ( $ℓ = 3$ )
	$m = 0$	$m = 0$	$m = \pm1$		$m = 0$	$m = \pm1$		$m = \pm2$		$m = 0$	$m = \pm1$		$m = \pm2$		$m = \pm3$
	s	p_z	p_x	p_y	d_z²	d_xz	d_yz	d_xy	d_x²−y²	f_z³	f_xz²	f_yz²	f_xyz	f_z(x²−y²)	f_{x(x²−3y²)}	f_{y(3x²−y²)}
$n = 1$
$n = 2$
$n = 3$
$n = 4$
$n = 5$										. . .	. . .	. . .	. . .	. . .	. . .	. . .
$n = 6$					. . . ‡	. . .	. . . ‡	. . .	. . . ‡	. . . *	. . . *	. . . *	. . . *	. . . *	. . . *	. . . *
$n = 7$		. . . †	. . . †	. . . †	. . . *	. . . *	. . . *	. . . *	. . . *	. . . *	. . . *	. . . *	. . . *	. . . *	. . . *	. . . *

* Haligacha 6f, 7d yoki 7f elektronli elementlar topilmagan. Bu holat esa, ularni yanada o'rganishga sabab bo'lmoqda.

7p elektronli elementlar topildi, ammo ularning elektron konfiguratsiyasi faqat taxmin qilingan xolos.

Eng baland orbitali 6d orbital boʻlgan elementlar uchun faqat ba'zi elektron konfiguratsiyalar tasdiqlangan. (Ds, Rg va Cn hali ham yo'q).

Bular kimyoda keng qo'llaniladigan haqiqiy qiymatli orbitallardir. Faqat $m=0$ orbitallar, bu yerda orbital burchak momentum operatorining xos holatlari, ${\hat {L}}_{z}$ . bilan ustunlar $m=\pm 1,\pm 2,\cdots$ Ular ikkita xos holatning kombinatsiyasini o'z ichiga oladi. Quyidagi rasmda taqqoslashni ko'ring:

Manbalar

↑ Orchin, Milton. Atomic Orbital Theory, 2005.
↑ Daintith, J.. Oxford Dictionary of Chemistry. New York: Oxford University Press, 2004. ISBN 978-0-19-860918-6.
↑ Griffiths, David. Introduction to Quantum Mechanics. Prentice Hall, 1995 — 190–191-bet. ISBN 978-0-13-124405-4.
↑ Levine, Ira. Quantum Chemistry, 5, Prentice Hall, 2000 — 144–145-bet. ISBN 978-0-13-685512-5.
↑ Laidler, Keith J.. Physical Chemistry. Benjamin/Cummings, 1982 — 488-bet. ISBN 978-0-8053-5682-3.
↑ Atkins, Peter. Quanta, Matter, and Change: A Molecular Approach to Physical Chemistry. Oxford University Press, 2009 — 106-bet. ISBN 978-0-19-920606-3.
↑ Gerlach, W.; Stern, O. (1922). „Das magnetische Moment des Silberatoms“. Zeitschrift für Physik. 9-jild, № 1. 353–355-bet. Bibcode:1922ZPhy....9..353G. doi:10.1007/BF01326984.

[1] Orchin, Milton. Atomic Orbital Theory, 2005.

[2] Daintith, J.. Oxford Dictionary of Chemistry. New York: Oxford University Press, 2004. ISBN 978-0-19-860918-6.

[3] Griffiths, David. Introduction to Quantum Mechanics. Prentice Hall, 1995 — 190–191-bet. ISBN 978-0-13-124405-4.

[4] Levine, Ira. Quantum Chemistry, 5, Prentice Hall, 2000 — 144–145-bet. ISBN 978-0-13-685512-5.

[5] Laidler, Keith J.. Physical Chemistry. Benjamin/Cummings, 1982 — 488-bet. ISBN 978-0-8053-5682-3.

[6] Atkins, Peter. Quanta, Matter, and Change: A Molecular Approach to Physical Chemistry. Oxford University Press, 2009 — 106-bet. ISBN 978-0-19-920606-3.

[7] Gerlach, W.; Stern, O. (1922). „Das magnetische Moment des Silberatoms“. Zeitschrift für Physik. 9-jild, № 1. 353–355-bet. Bibcode:1922ZPhy....9..353G. doi:10.1007/BF01326984.

[1]

[2]

[3]

[4]

[5]

[6]

[7]